Вывод уравнения движения сплошной среды в координатах Эйлера 

А.Ю.Дроздов 

За основу нашего вывода берём формулу (7) главы 2.9 теории упругости Новацкого, стр. 64. 

В левой части материальная (местная) производная скорости материальной частицы по времени. 

Для преобразования материальной производной используем уравнение (5) главы 2.8 той же книги, стр. 60 

Здесь первый член правой части описывает изменение во времени функции при постоянном ξ т.е. при неизменном положении в пространстве, а не для одной и той же материальной частицы. Второе слагаемое правой части называется конвективной производной. Здесь нужно иметь в виду, что формула (5) главы 2.8 Новацким получена "ограничиваясь величинами первого порядка малости по dt" разложения Тейлора от  

То есть если ограничиться величинами хотя бы второго порядка малости по dt, то в уравнении движения сплошной среды появится ещё один источник нелинейности. 

О скорости материальной частицы в описании Эйлера Новацкий пишет следующее: "В этом описании движение тела представляестя векторным полем , связанным с мгновенным положением материальной частицы." Однако, к сожалению, в работе Новацкого отсутсвует взаимосвязь скорости со смещением в описании Эйлера. Попробуем восполнить этот пробел. Для этого применим рассуждение Новацкого о вычислении материальной производной такой характеристики материальной среды как начальная координата частицы среды  

Первое слагаемое правой части представляет собой изменение во времени функции (начальной координаты частиц среды) при неизменном положении в пространстве, а не для одной и той же материальной частицы. Но поскольку мы выводим уравнение движения сплошной среды, в основе которого лежит второй закон Ньютона, нам необходимо изменение во времени координат частиц среды именно для одной и той же материальной частицы. Именно в связи с этим возникает необходимость второго слагаемого: материальной (конвективной, субстанционной) производной. 

Переносим конвективную производную в левую часть 

Раскрываем знак суммы 

Раскрывая индекс i, переписываем в форме системы уравнений 

В матричной форме  

Выразим координату начальной точки среды через перемещения 

Для описания Эйлера 

Дифференцируем ее по координате Эйлера 

Дифференцируем по времени 

Подставляя в матричную систему уравнений, имеем 

Решая систему, получаем выражение для скорости материальных частиц в зависимости от смещения в описании Эйлера 

Решение в общем виде, полученное Методом Крамера 

Проблема полученных формул, кроме их громоздкости, однако та, что если перемещения по одной или по двум координатам равны нулю, например в случае плоской волны (продольной или поперечной) то детерминант матрицы будет равен нулю, что приведёт к нулю в знаменателе. Поэтому в дальнной работе ниже представлена процедура вычисления скорости материальной частицы

Приступаем к непосредственному выводу уравнения движения 

(1)

 

координаты Эйлера 

(2)

 

вектор перемещения 

(3)

 

Заполняем матрицу производной смещения по координатам Эйлера 

>

 

(4)

 

Вектор правых частей - производня смещения по времени 

(5)

 

Определяем процедуру определения скорости материальных частиц в зависимости от смещения в описании Эйлера 

В общем случае 

Для конкретного случая из общего выражения для скорости  

Скорость среды в координатах Эйлера для плоской волны вычисляем более упрощённо 

Например. 

Для случая плоской продольной волны, распространяющейся вдоль оси X,  получаем 

(6)

 

(7)

 

(8)

 

Для случая плоской поперечной волны, распространяющейся вдоль X, колебания частиц среды в которой происходят вдоль оси Z 

(9)

 

(10)

 

(11)

 

А это пример поперечной волны, распространяющейся вдоль оси Y, колебания частиц среды, в которой происходят вдоль оси X 

(12)

 

Объявляем матрицу для тензора Альманси 

>

 

>

 

>

 

>

 

(13)

 

Символ Кронекера 

>

 

(14)

 

Общее выражение для закона Гука - заполняем матрицу тензора напряжений
 

>

 

(15)

 

Заполняем матрицу тензора Альманси 

>

 

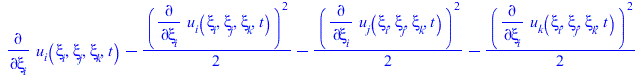(16)

 

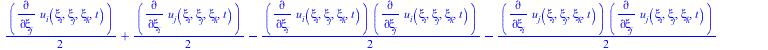(17)

 

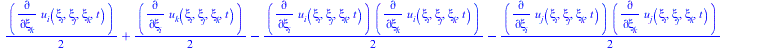(18)

 

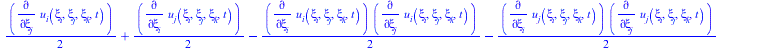(19)

 

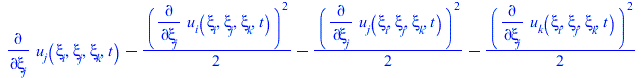(20)

 

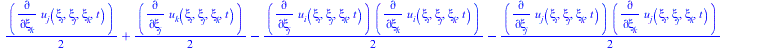(21)

 

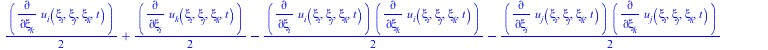(22)

 

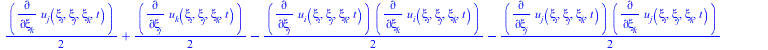(23)

 

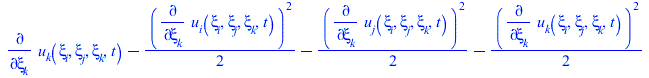(24)

 

Определяем процедуру заполнения тензора Альманси 

>

 

(25)

 

>

 

(26)

 

>

 

(27)

 

В матрицу тензора напряжений подставляем тензор Альманси 

>

 

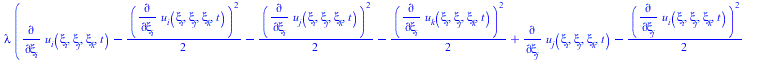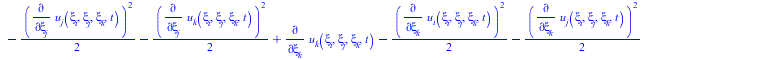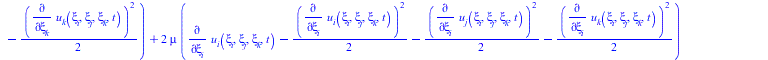(28)

 

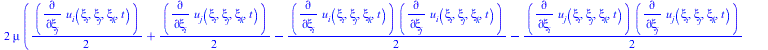(29)

 

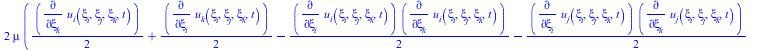(30)

 

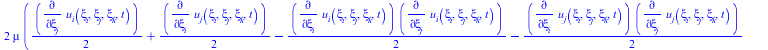(31)

 

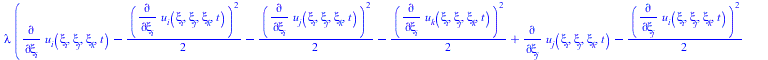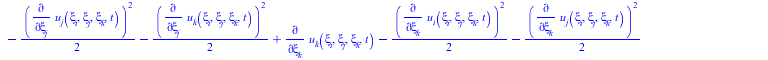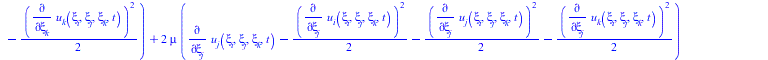(32)

 

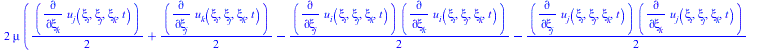(33)

 

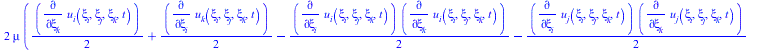(34)

 

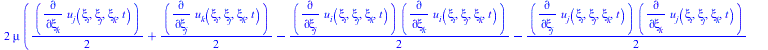(35)

 

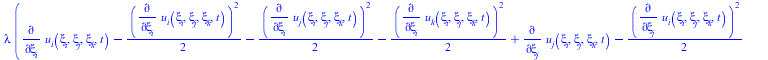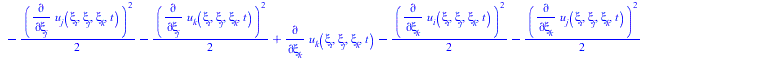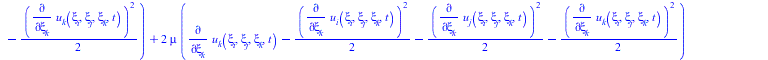(36)

 

Определяем процедуру вычисления тензора напряжений на основе тензора Альманси 

(37)

 

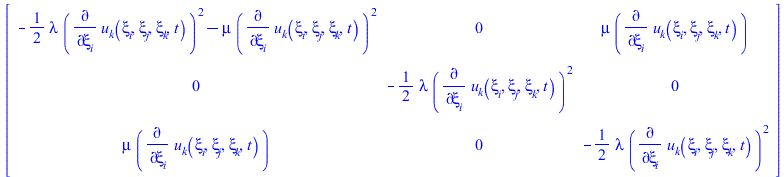(38)

 

Сила, действующая на элемент объёма 

>

 

Определяем процедуру вычисления силы, действующей на элемент объёма, исходя из тензора напряжений 

(39)

 

(40)

 

Уравнение движения с учётом конвективной производной покомпонентно 

Введём функцию плотности 

(41)

 

Определим процедуру формирования системы дифференциальных уравнений движения с учетом конвективной производной скорости материальных частиц а также включая уравнение непрерывности 

Теперь сформируем систему дифференциальных уравнений для продольной волны 

(42)

 

сформируем систему дифференциальных уравнений для поперечной волны 

(43)

 

Полученные уравнения носят явно нелинейный характер 

Чтобы в этом убедиться попробуем подставить синусоиду в систему уравнений для плоской продольной волны 

(44)

 

попробуем подставить синусоиду в систему уравнений для плоской поперечной волны 

(45)

 

И что же невооружённым глазом видно что синусоида не удовлетворяет уравнению плоской волны: ни продольной ни поперечной. Что говорит о нелинейности действительного уравнения движения сплошной среды, в отличие от уравнения Ламе, вывод которого даётся в курсах линейной теории упругости.