Размышления на тему теории упругой вселенной Чурляева - продолжение 

А.Ю.Дроздов 

Резюмирую материал, представленный Размышления на тему теории упругой вселенной Чурляева могу сказать следующее.

Волновым уравнением вакуума, которому могут удовлетворять решения в виде сферических стоячих волн, в первом (линейном) приближении является уравнение Ламе. Более точным волновым уравнением будет уравнение Ламе с учётом отброшенных нелинейных поправок: в тензоре Альманси и в выражении скорости через смещения в описании Эйлера. Такое уравнение, конечно же, нелинейно. Учёт этих нелинейностей позволит показать возникновение гравитационного поля частицы. Следующим этапом должно стать использование нелинейных уравнений движения моментной теории упругости. 

Проблемы с искуственностью введения закона наслоения у Чурляева возникли благодаря тому, что он в основе своей теории использовал неверное (простое) волновое уравнение. В данной работе я собираюсь показать, что сферическая стоячая волна, нормированная множителем при одновременном убывании частоты с расстоянием центра  как прекрасно удовлетворяет линейному уравнению Ламе. При этом может принимать дискретный спектр значений.

Таким образом закон наслоения с нелинейностью среды никак не связан. Он связан именно с необходимостью учесть объёмные деформации среды в сферической стоячей волне. 

Но тем не менее однородная по свойствам сплошная среда всё же нелинейна. И нелинейность эта связана тем что при выводе уравнения Ламе были отброшены бесконечно малые второго порядка. Так вот если учесть эти бесконечно малые, а именно, если вместо тензора деформации Коши использовать тензор деформации Альманси, то мы получим уже более приближённое к реальности уравнение сплошной среды.

Моё предварительное тестирование такого уравнения в декартовых координатах, показало что плоская продольная волна в такой среде уже не есть обычная синусоида! Хотя плоская поперечная - всё ещё синусоида.
 

Следующим шагом нужно будет от классической теории упругости с симметричными тензорами перейти к моментной теории братьев Коссеров, в которой тоже учесть нелинейный тензор Альманси. 

В данной работе я также показываю, что колебания в сферической стоячей волне могут быть направлены и в другом направлении (тороидальная мода колебаний)   

Начну с исследования поведения сферической стоячей волны, нормированную в соответствии с законом наслоения и с частотой убывающей как в среде, подчиняющейся уравнению Ламе 

выражение для сферической стоячей волны (Справочник по математике. Г.Корн и Т.Корн, стр. 327, 10.4-48) 

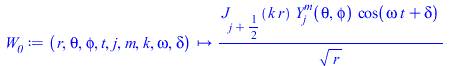(1)

 

Скалярную величину, как я это делал в случае волнового уравнения, мы не сможем исследовать, так как дивергенцию от скалярной величины взять не возможно. Поэтому в данной работе будем исследовать различные варианты направлений колебаний в локе 

Вариант Чурляева назначаем направления колебаний так, "чтобы все колебания были параллельны оси  Z" 

(2)

 

(3)

 

(4)

 

Определим вектор колебаний чурляевского решения волнового уравнения.  

Тороидальная мода колебаний из литературы https://pdfs.semanticscholar.org/a610/40a5032e5a59f0f6aa6a67b7f1b857224448.pdf в главе 2.1 "Shear oscillations of a perfectly elastic solid globe in the regime of standing waves of material displacements"
 

 

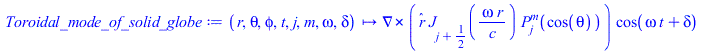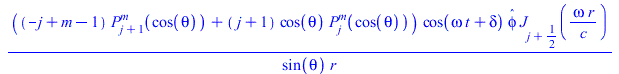	(5)

 

Сфероидальная мода колебаний оттуда же


 

 

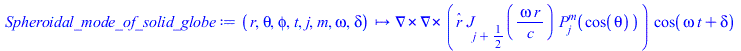	(6)

 

По аналогии с этими двумя модами колебаний из литературы мы можем назначить колебания не параллельно оси Z, а применив ротор к выражению сферической стоячей волны
Таким получаем тородально направленные колебания в сферической стоячей волне 

 

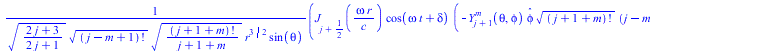	(7)

 

и сфероидально направленные колебания в сферической стоячей волне 

 

	(8)

 

Применим ко всем пяти модам колебаний нормировку по закону наслоения и по частоте, делённой на радиус

Чурляевский лок, нормированный по обратному радиусу и по частоте, делённой на радиус 

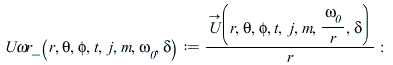
Тороидальная мода колебаний из литературы, нормированная по обратному радиусу и по частоте, делённой на радиус 

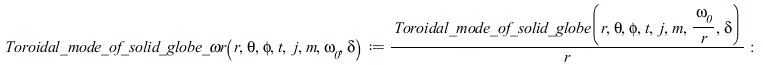
Сфероидальная мода колебаний из литературы, нормированная по обратному радиусу и по частоте, делённой на радиус 

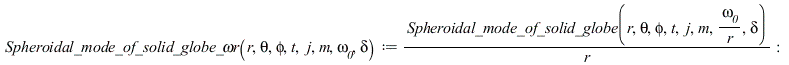
Тородальная мода сферической стоячей волны, нормированная по обратному радиусу и по частоте, делённой на радиус 

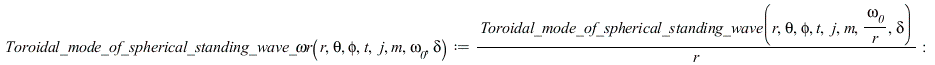
Сфероидальная мода сферической стоячей волны, нормированная по обратному радиусу и по частоте, делённой на радиус 

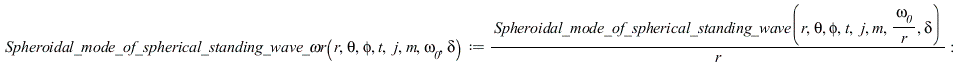
Определяем уравнение Ламе 

(9)

 

Чурляевский лок, нормированный по обратному радиусу и по частоте, делённой на радиус подставляем в уравнение Ламе 

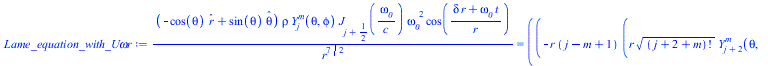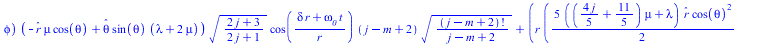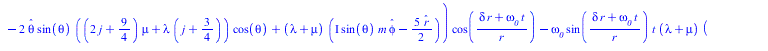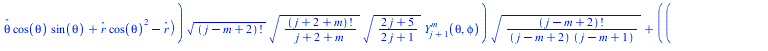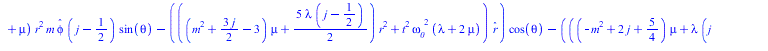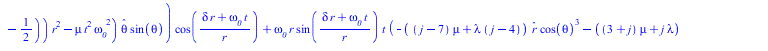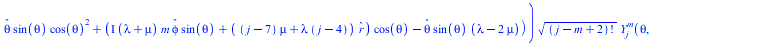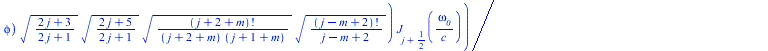(10)

 

Тородальную моду сферической стоячей волны, как есть - не нормируя,  подставляем в уравнение Ламе 

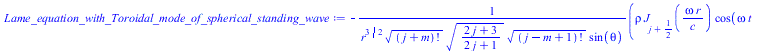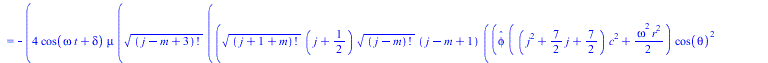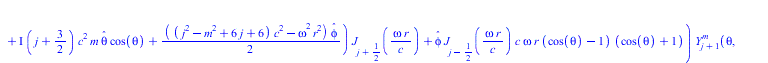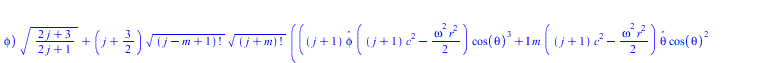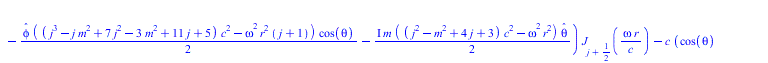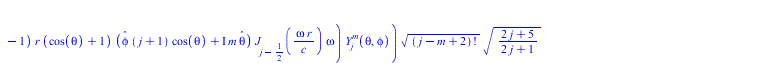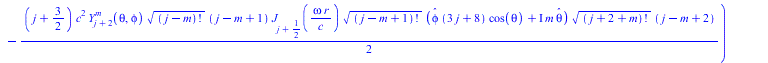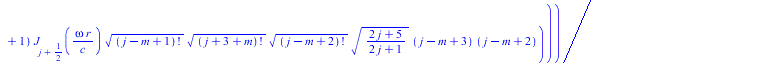(11)

 

Тородальная мода сферической стоячей волны, нормированная по обратному радиусу и по частоте, делённой на радиус  подставляем в уравнение Ламе 

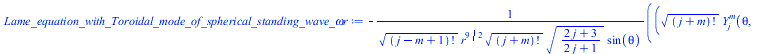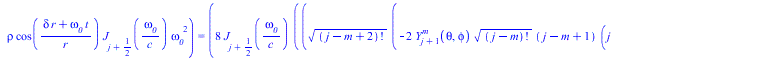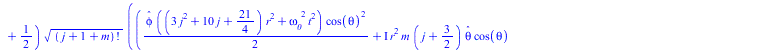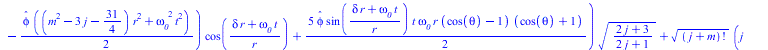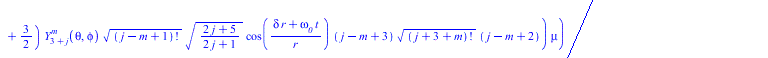(12)

 

Сфероидальную моду сферической стоячей волны, как есть - не нормируя,  подставляем в уравнение Ламе 

Тут я вычисления остановил - видимо слишком сложное выражение получается 

Сфероидальная мода сферической стоячей волны, нормированная по обратному радиусу и по частоте, делённой на радиус 

Решаем уравнение Ламе с подставленным Чурляевским локом, нормированным по обратному радиусу с частотой, обратно пропорциональной радиусу 

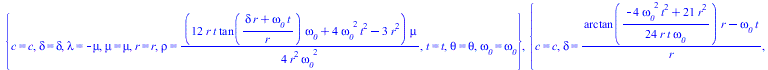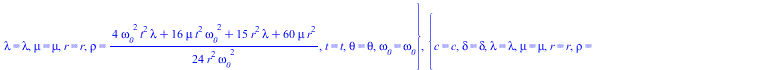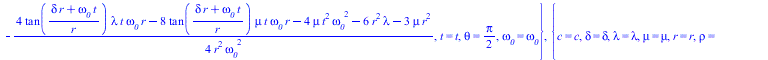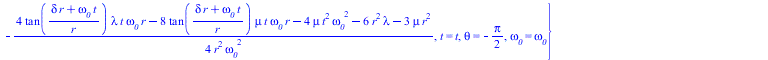(13)

 

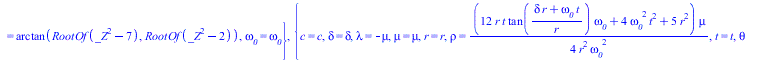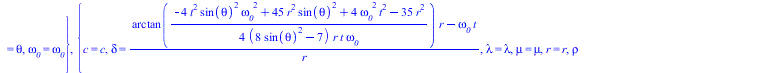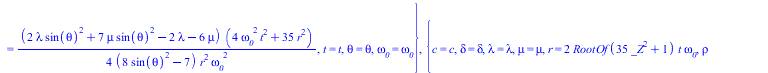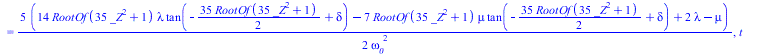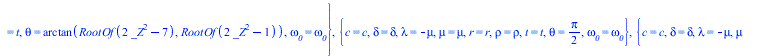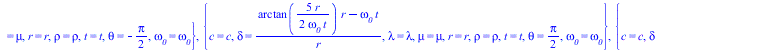(14)

 

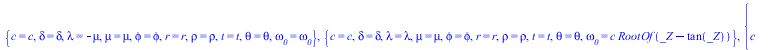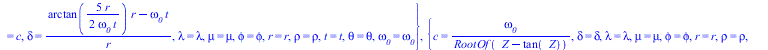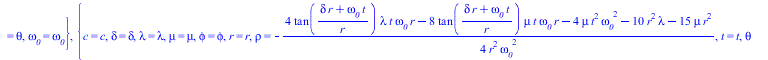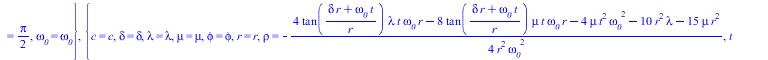(15)

 

Для лока 0,0 удовлетворительных решений не найдено

Но в предыдущей работе было найдено решение уравнение (107)








 

Если в данном решении положить  

тогда 

(16)

 

(17)

 

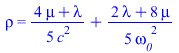(18)

 

(19)

 

Таким образом получается целый спектр решений с различными значениями базовой частоты и скорости  

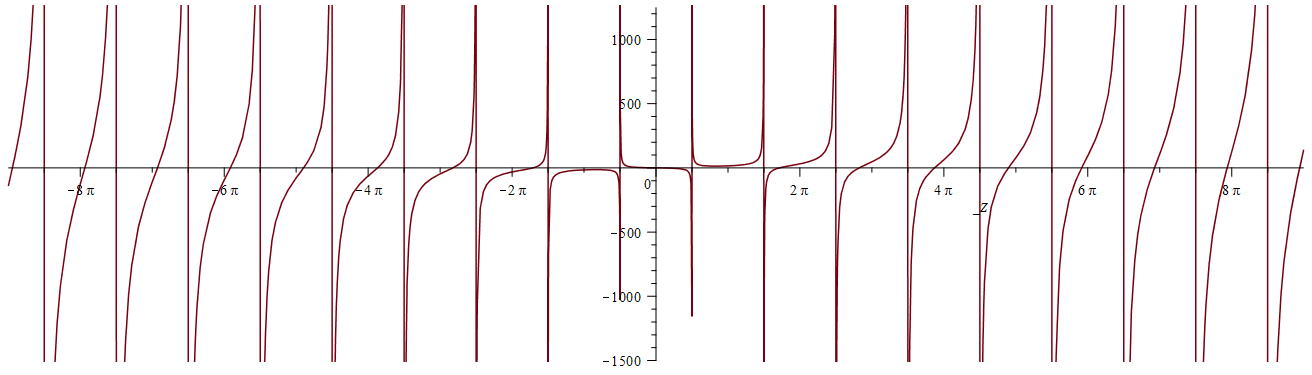Например 

(20)

 

(21)

 

(22)

 

(23)

 

Решение 1 

(24)

 

Решение 2 

(25)

 

Решение 3 

(26)

 

Для лока (1,0) найдено решение 

(27)

 

И аналогичное же решение найдено для лока (1,1) 

(28)

 

Таким образом сферическая стоячая волна, нормированная по обратному радиусу с частотой, обратно пропорциональной радиусу и с направлением колебаний параллельно оси Z удовлетворяет уравнению Ламе. Однако в случае волновых чисел 1,0 и 1,1 какой либо зависимости между скоростью, плотностью и упругими константами, к сожалению не обнаружено.  

Теперь решаем уравнение Ламе с тороидальной модой колебаний в сферической стоячей волне, нормированной по обратному радиусу с частотой, обратно пропорциональной радиусу 

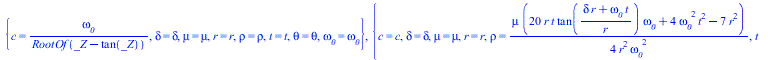(29)

 

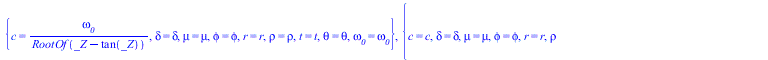(30)

 

(31)

 

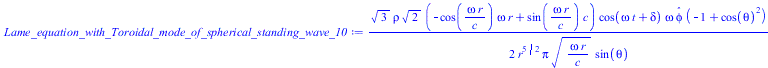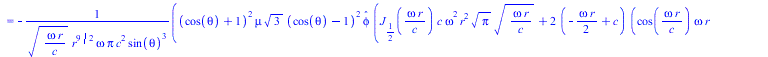(32)

 

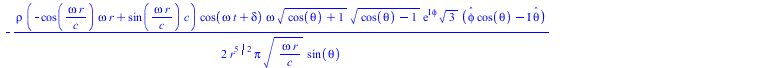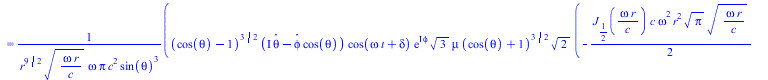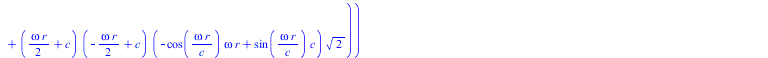(33)

 

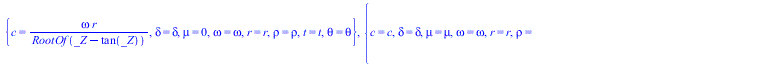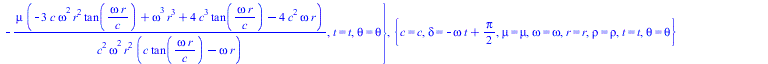(34)

 

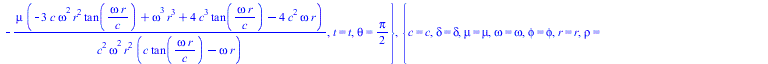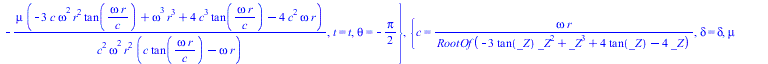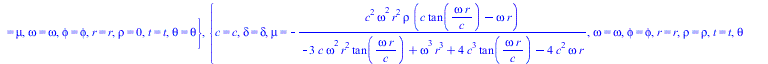(35)